Durante un momento de ocio que tuve entre cambio de clases, se me ocurrió la idea de desarrollar una aplicación que fuera capaz de buscar una cantidad n de números primos, después de informarme de las características de los números primos y de que técnicas se usan para poder determinar si un número es primo o no, entonces procedí a programar.
Para todos aquellos que no saben que es un número primo, es aquel que solo es divisible por 1 y por sí mismo, un ejemplo de ello es:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, …
Una de las maneras de determinar si un número es primo, es comprobar todos los números desde 2 hasta n-1, donde n es el número que estamos comprobando si es primo, pero esto se hace un proceso lento y que consume muchísimos recursos computacionalmente hablando, por lo que una manera de reducir el número de comprobaciones es solamente comprobando desde 2 hasta la raíz cuadrada de n. En caso de que la raíz no sea exacta, entonces se tomara el número entero más cercano.
Pero aun así el proceso es lento, por ejemplo si queremos determinar si el número 179424673 es primo, tendríamos que comprobar entre 2 y 13395 (que es el número entero más cercano a la raíz cuadrada de 179424673), lo que es aún una gran cantidad de operaciones, por lo tanto es una excelente idea almacenar los números primos que vamos obteniendo en alguna estructura de datos, en este caso la estructura que elegida fue una Lista Ligada en donde se prioriza la velocidad para almacenar nuevos datos. Si bien no es la mejor estructura para la búsqueda de información, esto no tiene una relevancia significativa, debido a que la búsqueda es de manera secuencial, por lo que no afecta el rendimiento general de la aplicación.
Volviendo al ejemplo anterior usando esta técnica de usar números primos para determinar si un número es primo reducimos drásticamente la cantidad de comprobaciones pasando de 13393 comprobaciones en caso de ir en aumentos de uno en uno o de 6697 comprobaciones en caso de ir probando solo con números impares, a solo 1600 comprobaciones, lo cual es una reducción drástica del número de comprobaciones.
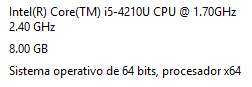
En mi caso uso la siguiente computadora:
Para ejecutar este programa se nos pedirán 3 entradas, la primera corresponde al número de números primos que se desean encontrar, el segundo corresponde al fichero de salida en donde se almacenaran los números primos encontrados (por defecto el formato de salida es txt) y el ultimo (opcional), corresponde al nombre y formato de un fichero en donde se han almacenado X números primos los cuales servirán de base para buscar otros números primos. La idea principal de poder cargar un fichero, es evitar la pérdida de tiempo en caso de que se tengan X números primos y solo se desee ampliar la cantidad. Si no se tiene ningún fichero previo, solo ingresar al menos un carácter, y el programa continuara con su ejecución.
Obteniendo los siguientes resultados:
Búsqueda de los primeros 100 Millones de Números Primos
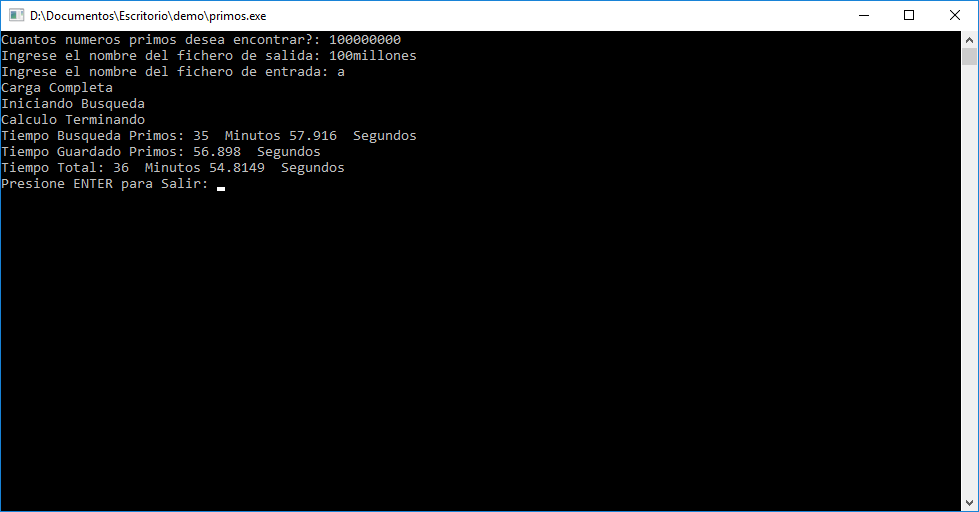
En este caso el proceso completo tardo 36 Minutos, usando según el administrador de Tareas de Windows uso 1.8 Gb de Memoria RAM y entre el 30% y el 45% del Procesador.
Búsqueda de los primeros 10 Millones de Números Primos
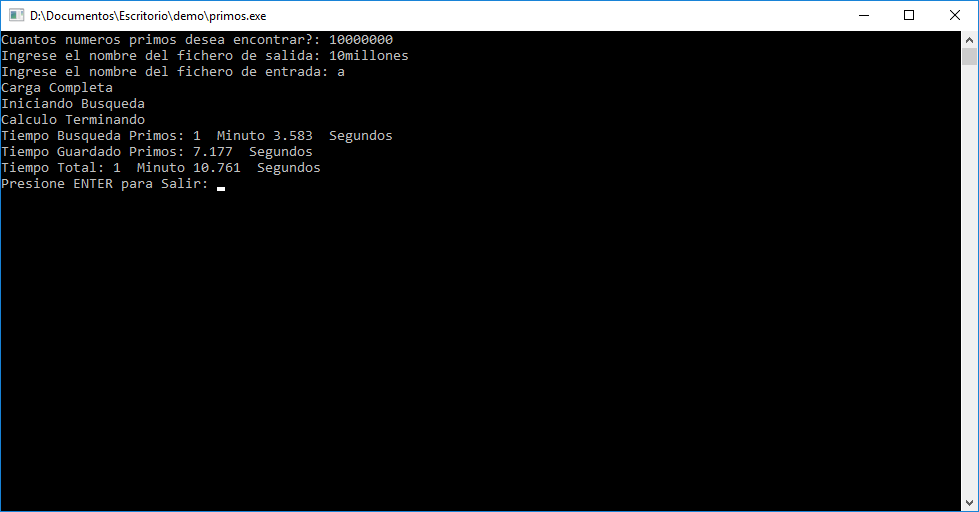
En esta otra oportunidad el proceso tardo aproximadamente 1 minutos, uso 160 MB de Memoria RAM y entre el 30% y el 45% del Procesador.
Búsqueda del primer Millones de Números Primos
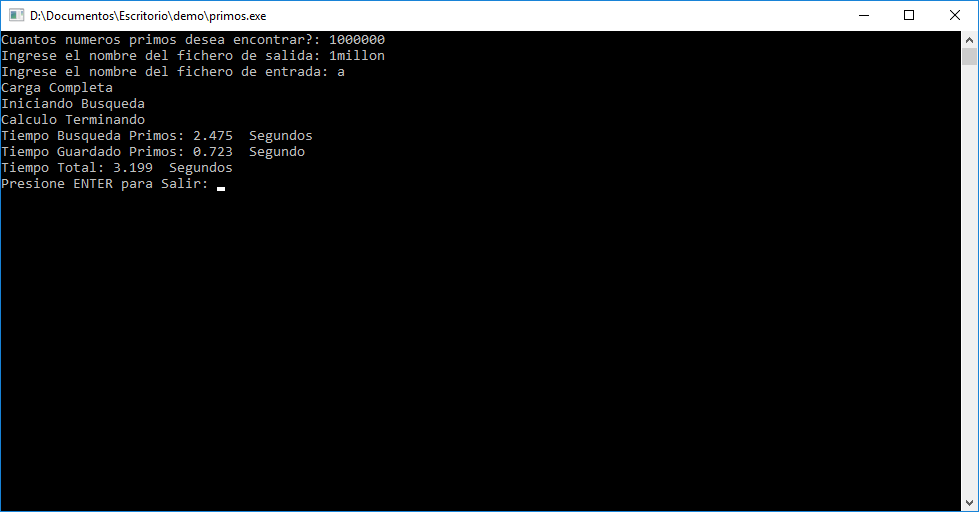
En esta otra oportunidad el proceso tardo aproximadamente 3 segundos, uso 12 MB de Memoria RAM y entre el 30% y el 45% del Procesador.
Descargas
Descargar Código en CPP y EXE desde Github
Primeros 10 Millones de Números Primos TXT (Comprimido con 7z)
Primeros 100 Millones de Números Primos TXT (Comprimido con 7z)
Dado que el archivo TXT es muy pesado de más de 1 Gb, necesitaras de un lector que sea capaz de poder abrir este tipo de archivos, por lo que les recomiendo EmEditor, el cual lo pueden descargas desde la siguiente pagina.
